Model setup¶
Model definition¶
The Cook membrane problem is a classic benchmark test which is used to check for shear-locking behaviour under incompressible conditions. In this study, a linear material model with two different Poisson’s ratio values of 0.3333 and 0.4999 has been tested. It is expected that the solvers will face some difficulties to compute solution, especially for the latter value.
The other purpose of this benchmark is to check if an FE code allows to apply a force distributed over area in shear direction. While a pressure definition (normal force over area) is very popular loading condition among all FE codes, the variation with direction tangential to the surface is not that common.
It should be noted that in this study, the three-dimensional geometry has been modelled. Number of variations of this benchmark can be found in the literature, but in this example the thickness of 5mm has been assumed.
Tip
The benchmark geometry shown above is interactive and it shows displacement in vertical direction [mm].
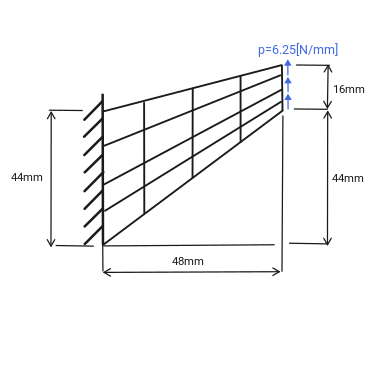
Fig. 10 Sketch of the Cook’s membrane benchmark¶
Target solution¶
As per the source, the target solution for this benchmark is:
32.00 mm for Poisson’s ratio of 0.3333
28.00 mm for Poisson’s ratio of 0.4999
Material properties¶
Property |
Value |
Unit |
|---|---|---|
Young’s modulus, E |
70.00 |
Pa |
Poissons ratio, \(\nu\) |
0.3333 / 0.4999 |
- |
Boundary conditions¶
The membrane considered in this study is fixed at its’ left side (the dimension 44 mm in the picture above) and the symmetry condition in out-of-plane direction is also assumed.
The model is driven by the distributed force of \(6.25 N/mm\) applied to right side of the geometry.
